Introduction: When Correct Answers Hide Confusion

Many students can count fluently.
They follow procedures accurately and often arrive at the correct answers.
Yet, when asked a simple question:
“Which number is closer to 1,000: 972 or 1,028?”
Some guess.
Some immediately subtract.
Very few instantly recognise that both numbers are equally close.
This is not a small error.
It reveals a deeper problem—weak number sense.
The Hidden Truth: Numbers Are Abstract

One fundamental truth remains constant throughout mathematics education:
A number is not the symbol written on paper.
A number is the meaning behind that symbol—an abstract idea representing quantity or magnitude. Numbers cannot be touched or seen. What students interact with are representations of numbers, not the numbers themselves.
When mathematics instruction focuses only on symbols and procedures, the meaning behind those symbols slowly disappears.
Digit, Numeral, and Number: A Distinction That Matters

Confusion often begins when three distinct ideas are treated as the same:
- Digits are symbols: 0–9
- Numerals are written representations: 472, four hundred seventy-two, CDLXXII
- Numbers are abstract ideas of quantity and size
This distinction is essential at every stage of learning. True fluency develops from understanding numbers—not from memorising numerals or manipulating symbols.
Why Procedural Fluency Is Not Enough
Many students can:
- Perform calculations correctly
- Memorise steps and formulas
- Apply algorithms accurately
Yet they struggle with:
- Estimation
- Mental mathematics
- Sense-making
- Judging whether an answer is reasonable
This happens when procedures develop faster than understanding. Number sense is not a skill that ends after learning to count—it must grow continuously across grades.
Visualization: A Core Mathematical Tool
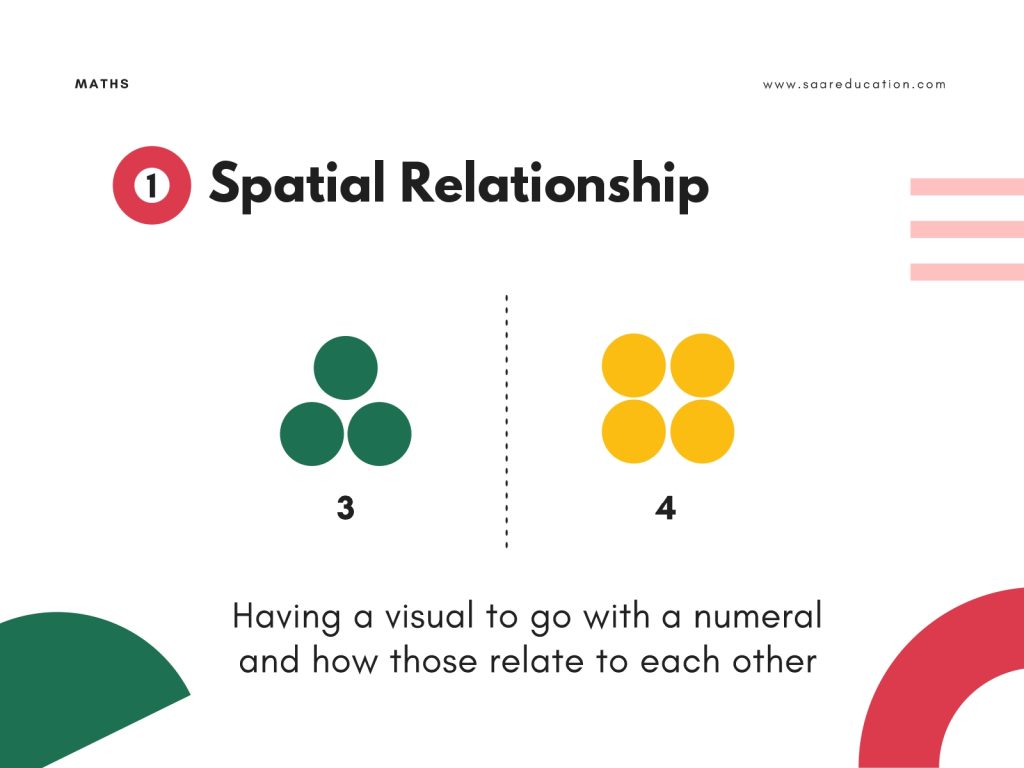
Visualization is not just for early learners.
- Young children use dots, counters, and objects
- Older students rely on number lines, arrays, and area models
Seeing:
- 748 as 700 + 40 + 8
- 36 × 4 as 36 groups of 4
builds conceptual clarity. Visual representations make the meaning of numbers and operations visible, supporting deeper understanding across age groups.
More and Less: From Counting to Reasoning

The ideas of one more, two more, one less, and two less evolve over time:
- Early learning: one more than 7
- Later learning: one more than 999
These relationships help students understand how quantities change—not just how to compute answers. This shift from counting to reasoning is a key component of strong number sense.
Benchmarks: Anchors for Mathematical Thinking
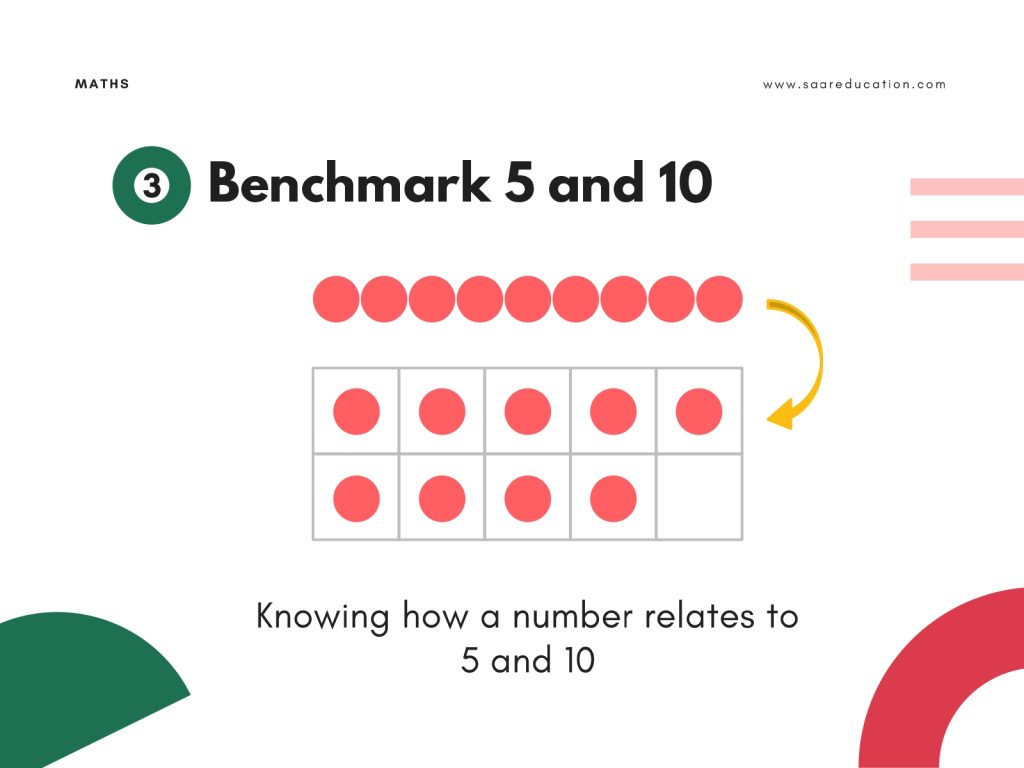
Benchmarks allow learners to reason efficiently and flexibly.
Common benchmarks include:
- 5 and 10
- 100 and 1,000
Recognising that 972 and 1,028 are both 28 away from 1,000 is a benchmark-based insight—not a procedural one.
Benchmarks support:
- Estimation
- Logical reasoning
- Detecting unreasonable answers
Part–Part–Whole: The Heart of Mathematics
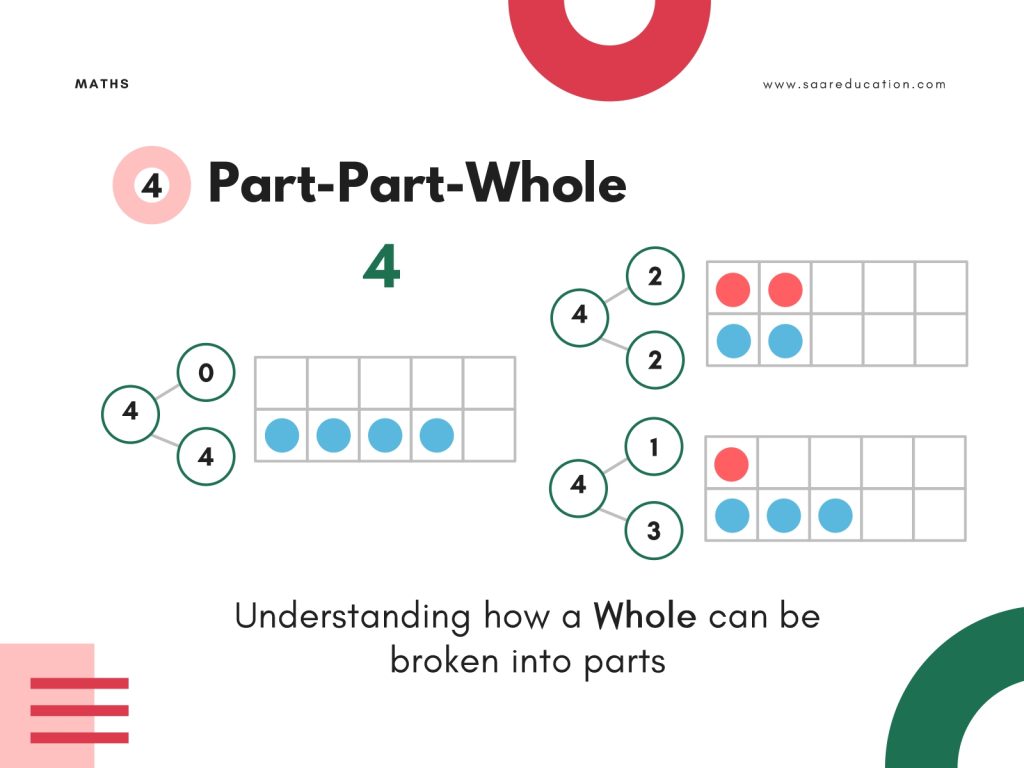
At the core of number understanding lies one powerful idea:
Every number can be broken into parts and recomposed.
Examples include:
- 8 = 5 + 3
- 1,000 = 700 + 300
- 45 × 6 = (40 × 6) + (5 × 6)
This way of thinking underpins:
- Addition and subtraction
- Multiplication
- Place-value understanding
Students who see structure think more flexibly, reason more deeply, and approach mathematics with confidence.
The Real Problem — and the Shift Needed
❌ Teaching mathematics as rules to apply
✅ Teaching mathematics as relationships to understand
Students must clearly grasp that:
- Digits are symbols
- Numerals are representations
- Numbers are ideas that can be reasoned with
Only then do procedures become meaningful tools rather than mechanical steps.
Final Thought
True mathematics begins when learners understand numbers beyond symbols and steps.
When digits, numerals, quantities, and relationships are connected through visualization, benchmarks, and structure, students don’t just calculate—
They think mathematically.