For generations, children have confidently recited multiplication tables:
Two ones are two
Two twos are four
Two threes are six…
Fluency improves. Answers come faster.
Yet something deeply important is missing.
Many students—and even adults—do not know what they are actually saying.
This is not a failure of arithmetic.
It is a failure of language, meaning, and structure.
The Core Problem: We Memorise Sounds, Not Structure
In most classrooms and explanations, multiplication is reduced to:
- chanting tables,
- calling it “repeated addition,”
- and quickly saying, “order doesn’t matter.”
While numerically correct, this approach erases meaning.
Multiplication is not just fast addition.
It is a relationship between two different roles:
multiplier x multiplicand= product
Where:
- multiplicand = the size of each group
- multiplier = the number of groups
This distinction is conceptual, not cosmetic.
The Most Common Mistake: “The First Number Is the Multiplicand”
You will often hear statements like:
- “In 8 × 2, 8 is the multiplicand.”
- “The bigger number is the multiplicand.”
- “It doesn’t matter anyway—order is the same.”
All three are conceptually incorrect.
In an equal-groups situation:
- 8 × 2 means 8 groups of 2
- 2 is the multiplicand (what is being repeated)
- 8 is the multiplier (how many times it is repeated)
This is not a personal preference. Mathematics education research clearly states:
“In equal groups situations, the number of objects in each group is the multiplicand, and the number of groups is the multiplier.”
— Sum & Kwon (2018)
How Language Makes It Worse
English allows multiple—and often conflicting—phrases:
- “Three times four”
- “Three multiplied by four”
- “Four threes are twelve”
- “Three fours are twelve”
Each phrase triggers a different mental image.
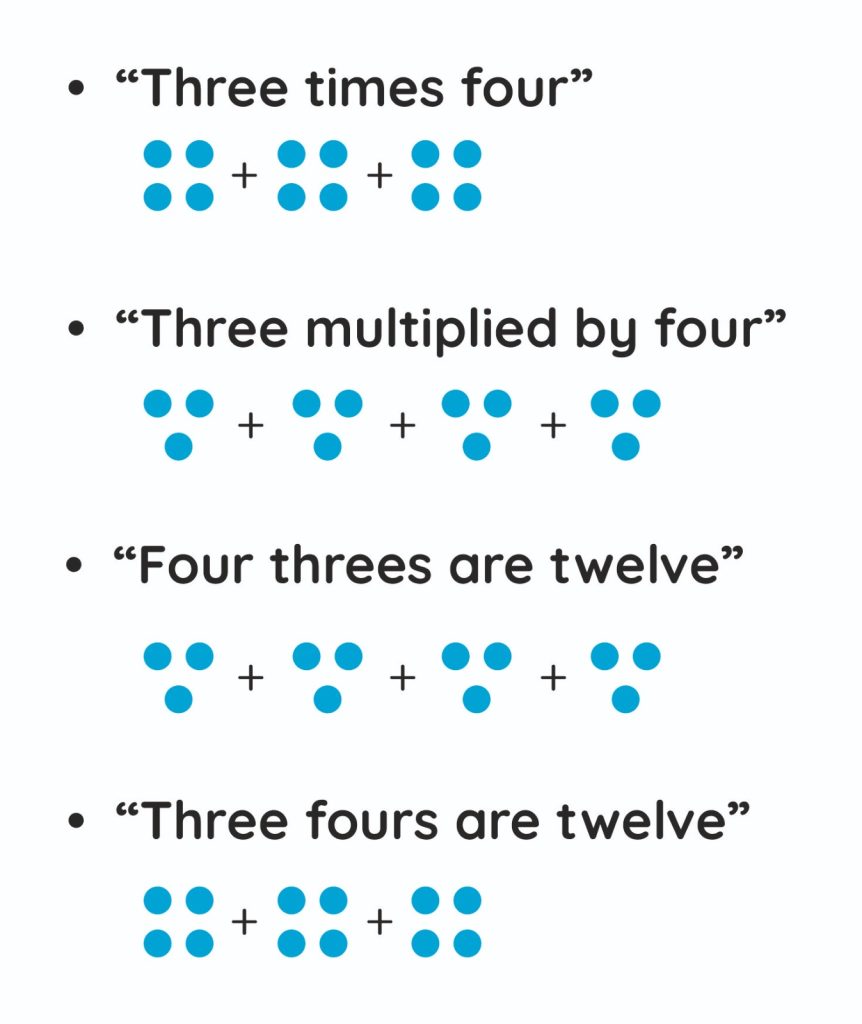
Research in mathematics and language shows that such ambiguity:
- increases confusion,
- hides structure,
- and promotes procedure without understanding.
Children learn what to say, not what it means.
NCERT Gets This Right
NCERT textbooks, especially Class 2, Chapter 8, use precise and consistent language:
- “Seven fours are twenty-eight”
- “How many fours are you adding?”
https://www.saareducation.com/app/books/get_flip_book_preview/2473
They begin with visual groups, move to spoken meaning, and only then introduce symbols.
This sequencing prevents confusion between the roles of numbers.
Visual Clarity Matters: Consistency in Grouping

A helpful example from SAAR Education highlights why visuals matter as much as words.
✅ Consistent Representation
- 1 × 2, 2 × 2, 3 × 2
- The group size stays the same
- The number of groups increases
This aligns perfectly with the idea of repeated addition.
⚠️ Inconsistent Representation
- 2 × 1, 2 × 2, 2 × 3
- The number of groups remains fixed
- The group size changes
Although mathematically valid, this representation confuses beginners about what is repeating.
Key insight:
If we teach multiplication as repeated addition, the visuals must reflect what is repeating and what is changing.
Why “Order Doesn’t Matter” Is Dangerous—Too Early
Yes, numerically:
- 3 × 4 = 4 × 3
But cognitively:
- they do not mean the same thing to a child.
Research confirms:
“Multiplication is psychologically non-commutative in problem contexts.”
— Greer (1992)
When commutativity is emphasized too early, children struggle with:
- word problems,
- division,
- ratios,
- and later algebraic thinking.
Understanding must come before shortcuts.
A Better Way to Explain Tables
Instead of saying:
“Two threes are six”
Try:
- “Two groups of three make six.”
- “Three added two times is six.”
- “The group size is three, and there are two groups.”
This language builds accurate mental models and prepares learners for:
- division,
- fractions,
- ratios,
- proportional reasoning.
Final Thought
Multiplication tables are not the problem.
The way we explain them often is.
If we want children to truly understand mathematics, we must move beyond chants and speed.
The multiplicand is what stays the same in every group.
The multiplier tells us how many times that group appears.
Anything else is noise.