
The Case for Number Bonds in the Early Mathematics Curriculum
Introduction
In many early mathematics classrooms, children are introduced to vertical addition algorithms—stacking numbers and carrying—before they have developed robust number sense. While these procedures can efficiently produce correct answers, their premature introduction comes at a significant cognitive cost.
Research in mathematics education consistently shows that conceptual understanding must precede procedural fluency. When algorithms are taught too early—especially without foundational experiences such as number bonds—children’s intuitive understanding of numbers and their relationships is weakened. Over time, this undermines flexibility, reasoning, and long-term mathematical confidence.
Procedural Fluency Without Conceptual Understanding
A simple example highlights this concern clearly: 9 + 6.
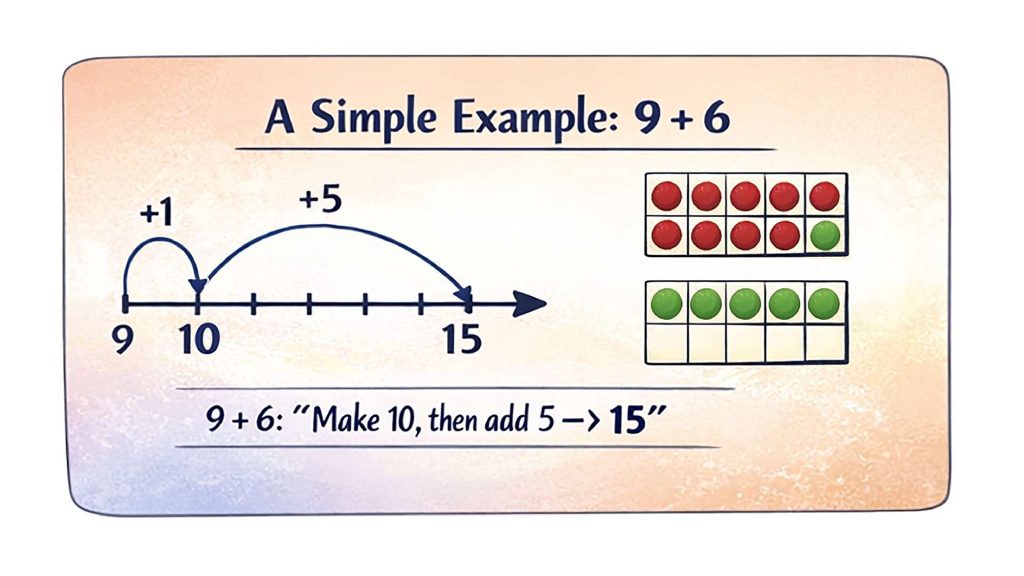
Rather than immediately presenting this as a vertical addition problem, developmentally appropriate instruction encourages children to reason intuitively using strategies such as:
- Counting on from the larger number (start at 9 and count 6 more)
- Recognising that 9 is one less than 10—a “friendly” number
- Decomposing 6 into 1 and 5
- Bridging through 10: add 1 to 9 to make 10, then add the remaining 5 to reach 15
These approaches reflect relational thinking—an understanding that numbers are flexible and interconnected.
A child might reason:
“9 needs 1 more to become 10. That leaves 5 from the 6. So 9 + 6 is 10 + 5, which equals 15.”
This reasoning explains why the answer works.
In contrast, when children are taught to stack numbers and “carry the 1” without context, the logic behind the process remains hidden. The algorithm produces an answer, but not understanding. Mathematics becomes a sequence of steps to memorise rather than a meaningful system of relationships.
Number Bonds: A Missing Conceptual Tool
Number bonds make the part–whole structure of numbers explicit. They help children understand that:
- Numbers can be composed and decomposed in multiple ways
- Addition and subtraction are inverse operations
- The same total can be represented through different combinations
- For example: 15 as 9 + 6 or 10 + 5
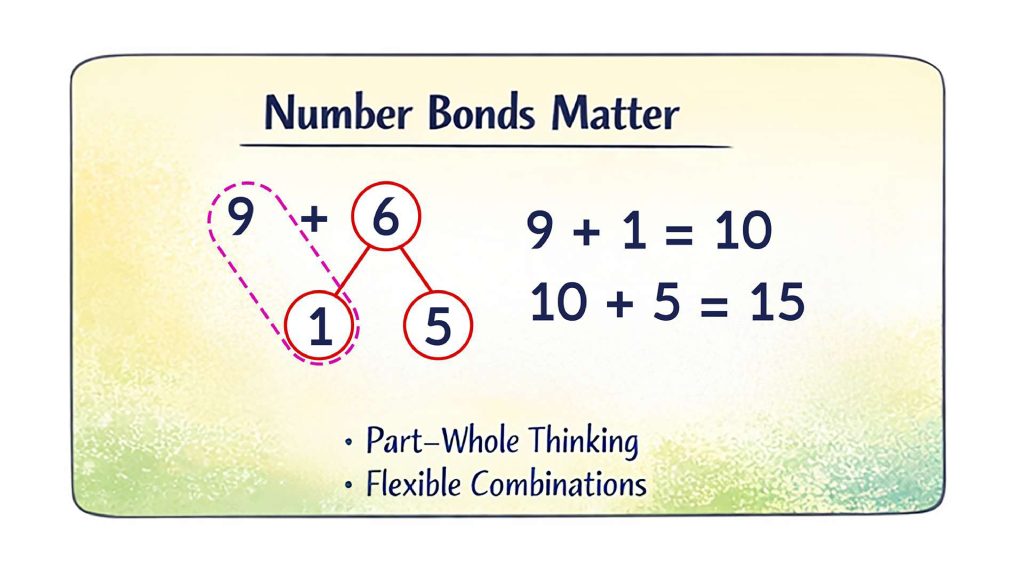
When number bonds are missing from instruction and textbooks, children often develop a rigid view of numbers. This limits their flexibility in mental computation and weakens estimation, reasoning, and problem-solving skills.
Impact on Mental Computation and Place Value
Mental strategies such as making ten or bridging through ten depend on a strong part–whole understanding.

Without visual and conceptual tools like number bonds:
- Strategies become memorised tricks rather than meaningful reasoning
- Place-value understanding remains fragile
- Regrouping becomes confusing
- Children over-rely on written algorithms for even simple calculations
This reliance signals not efficiency, but a lack of number sense.
Research and Curriculum Alignment
Research and high-performing education systems follow a clear instructional progression:
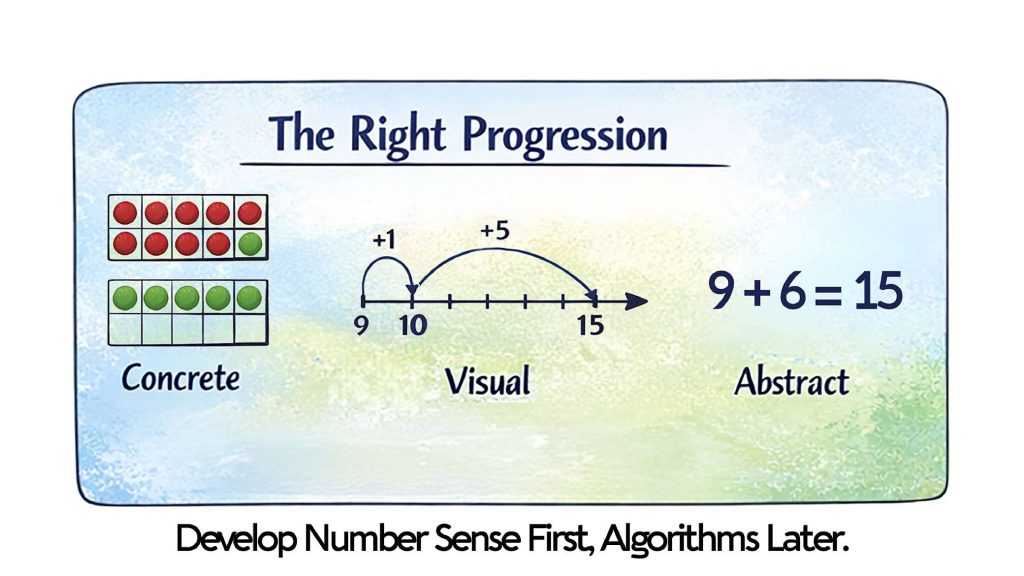
- Concrete experiences
- Visual representations
- Mental strategies
- Standard written algorithms
Introducing algorithms before this foundation reverses the learning sequence. The result is often superficial procedural competence instead of deep, transferable understanding.
Conclusion
Algorithms are valuable mathematical tools—but only when grounded in strong number sense. Number bonds are not optional visuals; they are essential cognitive structures that support flexible thinking, mental fluency, and conceptual understanding.
A curriculum that prioritises procedures over relationships may achieve short-term efficiency, but it sacrifices long-term mathematical learning. To build confident, capable, and resilient mathematicians, early mathematics instruction must foreground number relationships before formal algorithms.